MIT SCHACHBRETT UND FIGUREN MATHEMATISCHE PROBLEME LÖSEN
Von Christian Hesse
(Der Artikel ist auszugsweise wiedergegeben.
Den ganzen Beitrag lesen Sie in KARL 2/16)

Zwischen Mathematik und Schach bestehen viele Ähnlichkeiten. Schach ist annähernd so abstrakt wie Mathematik. Zwar spielt man es meist mit Figuren auf einem schwarz-weiß karierten 8×8-Brett. Doch genau besehen handelt es sich bei Brett und Figuren nur um verzichtbare Darstellungen einer Menge von 64 Punkten im zweidimensionalen Raum und einer Kollektion von Kräften, die auf diese Raumpunkte einwirken.
Die Schachfiguren symbolisieren also bestimmte Kräfte und deren Wirkungen benötigen keines physisch gegebenen Standfeldes, um sich zu entfalten. Die Art dieser Wirkungen ist durch die Spielregeln des Schachs festgelegt. Diese wurden von Menschen entwickelt und sind deshalb willkürlich. Genauso verhält es sich in der Mathematik mit den sogenannten Axiomen, den nicht beweisbaren Grundwahrheiten, die an den Anfang einer jeden mathematischen Theorie gestellt werden.
Viele Mathematiker haben sich vom Schachspiel inspirieren lassen. Das Spiel hat sie dazu angeregt, über Probleme nachzudenken, die es ohne Schachbrett und Figuren nicht gäbe. Umgekehrt begeistern sich viele Schachspieler auch für mathematische Probleme, Rätsel und Knobeleien.
Schon viel wurde über schachmathematische Probleme geschrieben und über die Techniken, mit denen man ihnen zu Leibe rücken kann. Also darüber, wie man Fragestellungen, die mit Schachbrett und Figuren zu tun haben, mit Methoden der Mathematik bearbeiten und schließlich lösen kann. Dazu gehören so faszinierende Aufgaben wie die Platzierung von sich nicht angreifenden Damen auf dem Schachbrett oder die Rundreise eines Springers über alle seine Felder.
Weit weniger Aufmerksamkeit wurde bisher dem in gewisser Weise genau umgekehrten Thema gewidmet, wie man bestimmte mathematische Problemstellungen mit Hilfe von schachlichen Accessoires, also mit Schachbrett und Figuren, lösen kann.
Das hört sich phantastisch, wenn nicht gar widersinnig, an. Und die erste Reaktion ist vielleicht: „Wie soll man Schachmaterialien und -konzepte zur Lösung mathematischer Probleme einsetzen können?“ Doch es geht, wie wir sehen werden. Denn genau dieser Bemühung ist der vorliegende Beitrag im Kern gewidmet.
PYTHAGORAS
Unsere erste mathematische Fragestellung ist der Satz des Pythagoras. Dieser Satz ist die wohl berühmteste Aussage der gesamten Mathematik. Sie besagt, dass in jedem rechtwinkligen Dreieck die Summe der Flächeninhalte der Katheten-Quadrate gleich dem Flächeninhalt des Hypotenusen-Quadrats ist. Oder eben mit der entsprechenden Beschriftung der Dreiecksseiten ganz einfach ausgedrückt als
a² + b² = c²
Für diese hübsche und nützliche Aussage gibt es mehr als 300 verschiedene mathematische Beweise. Einer findet sich in den Elementen des Euklid. Ein anderer geht sogar auf einen Staatsmann zurück. James Garfield (1831 – 1881), der vom 4.3.1881 bis zu einem Attentat, dem er am 19.9.1881 erlag, der 20. Präsident der Vereinigten Staaten war, blieb damit bis heute das einzige amerikanische Oberhaupt, das einen schöpferischen Beitrag zur Mathematik lieferte. Sein Beweis basiert auf dem folgenden Diagramm:
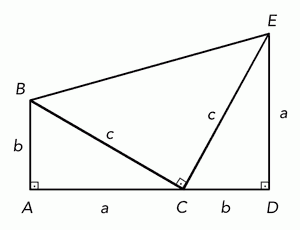
Sein Grundgedanke ist es, den Flächeninhalt des Trapezes ABED auf zwei Arten aufzuschreiben, zum einen mit der entsprechenden Flächeninhaltsformel:
![]()
Und zum anderen mit den Flächeninhaltsformeln für die das Trapez bildenden drei Dreiecke:
![]()
Gleichsetzen der Ausdrücke für den Flächeninhalt liefert
![]()
was nach Ausmultiplizieren und Zusammenfassen ergibt:
![]()
Nach Subtraktion von ab und Multiplikation mit 2 auf beiden Seiten ist man bei der angestrebten Gleichung. Ein hübscher und betörend einfacher Beweis.
Noch simpler ist Pythagoras zu haben, wenn man ein Schachbrett verwendet.

Die Fläche 1 ist ein rechtwinkliges Dreieck. Die Dreiecke 2, 3 und 4 sind kongruent zu diesem, also flächengleich. Wir sehen hier, dass der Flächeninhalt des Hypotenusen-Quadrats gleich dem Flächeninhalt des Schachbretts minus dem Flächeninhalt der vier Dreiecke ist.
Der Beweis ergibt sich nun ganz schlicht durch Umordnen dieser vier gleichgroßen Dreiecke.
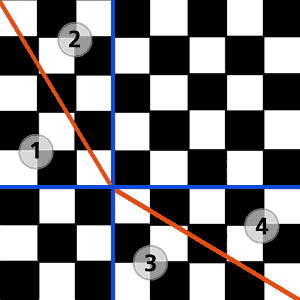
Dann ist der Flächeninhalt des Schachbretts minus dem Flächeninhalt der vier Dreiecke gleich dem Flächeninhalt der beiden Quadrate, deren Seitenlängen jeweils die Katheten jedes Dreiecks sind.
Also:
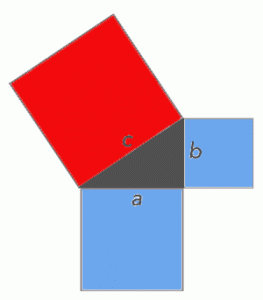
Und fertig. Schneller als die Fünf-Minuten-Terrine.
(Der Artikel ist auszugsweise wiedergegeben.
Den ganzen Beitrag lesen Sie in KARL 2/16)
